Semantic clustering of words with MajorClust and word2vec

In a recent project, I needed to arrange around a thousand words into semantic clusters. For this problem, the Vector Space Model seems well-suited. Previous research has released word vectors already trained on large text collections using methods like word2vec or GloVe. These vectors can be used to produce a similarity matrix, which can then be used for word clustering.

The first step is to obtain the word vectors, e.g. using the gensim library's downloader tool:

import pandas as pd
import numpy as np
import gensim.downloader as api

vectors = api.load("glove-wiki-gigaword-100")

Assuming the words one wants to cluster are in words, keep only relevant word vectors:

vectors = np.array([vectors[x] for x in words])

The next step is the choice of a clustering algorithm. While there are a few popular ones like K-means and DBSCAN, Majorclust is somewhat less known, but has an important advantage: it does not require stopping criteria like the number of clusters, the number of elements in a cluster, or the maximum distance between elements within a cluster, to be pre-set in advance: in many NLP tasks such as word clustering these are very hard to guess, even through lots of experimentation.

The algorithm is described in (Stein and Meyer zu Essen, 2002) in application to document clustering (see p.4 for pseudocode and explanation). Below is its Python implementation taken from here (cosine_matrix is a pre-computed matrix of document similarities):

# first assign each document to its own cluster
indices = np.arange(num_of_samples)
t = False
while not t:
    t = True
    # iterate over the documents
    for index in np.arange(num_of_samples):
        # find the cluster with the biggest similarity to the document
        new_index = np.argmax(np.bincount(indices, weights=cosine_matrix[index]))
        # if the cluster of the document has changed, iterate over the documents again
        if indices[new_index] != indices[index]:
            indices[index] = indices[new_index]
            t = False

In brief, the algorithm begins by assigning every document to its own cluster. At each iteration, each document gets assigned to the cluster, to which it has the biggest similarity. A document's similarity to a cluster is calculated as the sum of the document's cosine similarities to each of the cluster's members. Thus, a document can be re-clustered to other clusters at later iterations. Clustering stops when no document changes its cluster.

However I found that two modifications to this algorithm are necessary in my case. First, if many elements in the matrix have non-zero similarities to many other elements (e.g., word vectors have lots of non-zero values in the same columns, as is the case with word2vec vectors), then MajorClust may end up putting all elements into one single cluster. Therefore, it was necessary to introduce a threshold below which similarities get cancelled out, i.e. set to 0. After some experimentation I found that good results can be achieved by removing up to 99% of the smallest similarity pairs.

Second, after cancelling out low similarities, there will be many elements with no similarity to any other element. I.e., each of them should either constitute a cluster of its own or be treated as noise. MajorClust will merge two elements together even if the similarity between them is 0, thus producing one large catch-all cluster with lots of unrelated words. So the other modification is to prevent assigning an element to a cluster if its similarity equals zero.

The implementation below requires that all similarity values are equal or greater than 0, so first the features in the vectors need to be scaled to a range, e.g. (0, 1):

from sklearn.preprocessing import minmax_scale

vectors = minmax_scale(word_vectors, feature_range=(0, 1))

A similarity matrix can now be produced:

from sklearn.metrics.pairwise import cosine_similarity

def get_sim_matrix(X, threshold=0.9):
    """Output pairwise cosine similarities in X. Cancel out the bottom
    `threshold` percent of the pairs sorted by similarity.
    """
    sim_matrix = cosine_similarity(X)
    np.fill_diagonal(sim_matrix, 0.0)

    sorted_sims = np.sort(sim_matrix.flatten())
    thr_val = sorted_sims[int(sorted_sims.shape[0]*threshold)]
    sim_matrix[sim_matrix < thr_val] = 0.0

    return sim_matrix

sim_matrix = get_sim_matrix(vectors, 0.99)

The threshold parameter in the function represents the bottom percent of pairs to be cancelled out, after sorting the pairs by the cosine measure.

Now run Majorclust on the similarity matrix:

def majorclust(sim_matrix):
    """Actual MajorClust algorithm
    """
    t = False
    indices = np.arange(sim_matrix.shape[0])
    while not t:
        t = True
        for index in np.arange(sim_matrix.shape[0]):
            # check if all the sims of the word are not zeros
            weights = sim_matrix[index]
            if weights[weights > 0.0].shape[0] == 0:
                continue
            # aggregating edge weights
            new_index = np.argmax(np.bincount(indices, weights=weights))
            if indices[new_index] != indices[index]:
                indices[index] = indices[new_index]
                t = False
    return indices

labels = majorclust(sim_matrix)
word2clusters = dict(zip(words, labels))

The clustering result is word2clusters, a dictionary with words and their cluster ids.

With the modifications above, MajorClust came up with quite reasonable clusters like:

• car, vehicle, bike, truck, drive, driver, bus, helmet, cycle, motorcycle, pickup

• game, xbox, player, warfare, cod, dlc, battlefield, playstation, wii, nintendo, fifa, controller, sims, console, play, titanfall, ball, skyrim, gta, halo, gaming, ops, code, madden

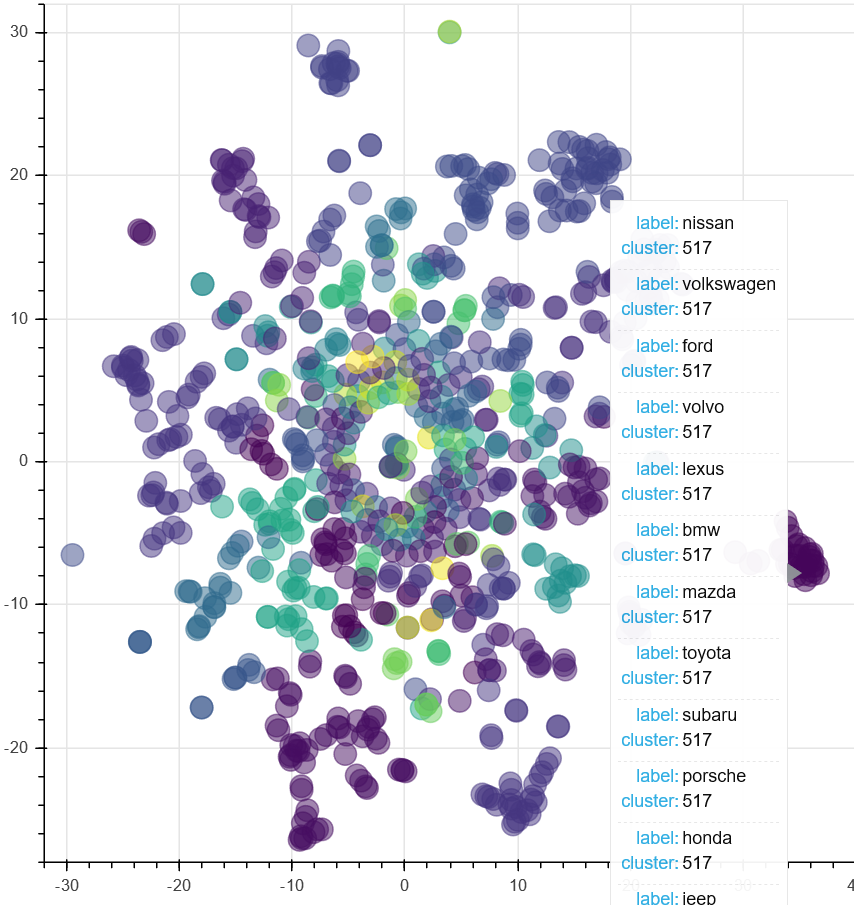
• ford, toyota, bmw, audi, honda, tesla, nissan, jeep, kia, suv, ferrari, range, mustang, chevy, subaru, skoda, lexus, porsche, lamborghini, hyundai, moto, mercedes, gmc, benz, rover, chevrolet, mazda, mower, golf, merc, jaguar, fords, turbo, tractor, duster, diesel, camry, gtr, volvo, auto, corvette, renault, dodge, datsun, volkswagen

• carrier, boat, flight, baggage, plane, drone, air, jet, back, trip, train, team, aircraft, balloon, yacht, space, cabin, fleet

• gun, datum, weapon, van, mag, ben, rifle, firearm, ammo, shotgun

• influence, supply, gas, power, petrol, fuel, electricity, boost, focus, booster, energy

Examples of words that ended up in singleton clusters: thing, brand, note, coin, item, box, case, pack, set, time, switch, machine. As one can see, these are words with many different meanings, so that it is hard to assign them to any particular semantic cluster.

Below is a t-SNE visualization of the clustered words (click the image for a zoomable graph).

The implementation of MajorClust used to derive these clusters, along with the scikit-learn API, can be found here.